This week, not only an age-old philosophical question for P4C and Maths, but a classroom match-report to give you ideas for facilitating it yourself.
r
The Stimulus
“What could this be?”
r
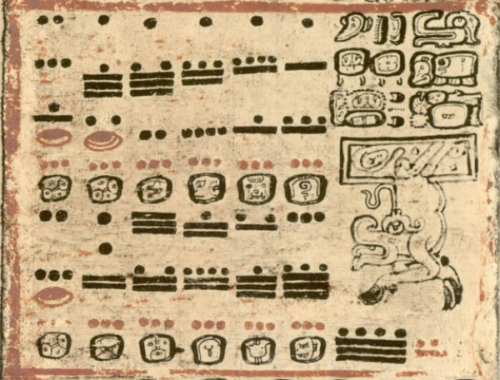
…is the question I asked Year 6 at St. Andrew’s Primary School last week, where I’m the Philosopher in Residence.
It’s actually the Mayan system of counting (see a more polished version here). The class were studying Mayans as a topic, and were moving on to Mayan numerals that very day.
The Mayan system was not influenced by, nor did it influence, other systems of mathematics, which led led me to think about the classic question: Was Mathematics invented, or discovered? There were a few things to do before letting Year 6 loose on it…
r
The Pre-thinking Thinking:
Some questions can have pupils buzzing with ideas from the first second. I’d tried this one ‘cold’ with a previous class, but many found it hard to get a foothold.
This time, half the class listed ‘inventions’ – defined as things humans had created, and the other half listed ‘discoveries’ – things that had been there before us. Establishment of these meanings are important not only to get this foothold, but also reach the crux of the question. It’s perfectly reasonable for something to be both an invention and a discovery: for example, a contraption invented by Romans, and found by us. However, we were looking at whether Mathematics existed before the first human. The relationship between the concepts of invention/discovery could easily have its own spin-off enquiry!
r
The Question: Was Mathematics invented, or discovered?
“There’s so many ways of coming at this…”
“This is really hard…”
With whiteboards away, and focus on each other, the class shared their thoughts. Part of my frantic scribblings are in the photograph below.

This is an example of the Scribe, Don’t Script principle explored in our Philosophy Circles training. Whilst the dialogue may be hard to follow when viewed isolation, in real time it provides pupils with a record of what’s been said, so they can more easily connect their thoughts to what’s already been proposed.
After the opening round of ideas (“you can’t touch Maths!” / “angles in a triangle always add up to 180 degrees”) one pupil suggested that Maths was always there, but we had invented numbers to describe it. 7 x 8 = 56 was true without us, but we decided to give it the labels of 7, 8 and 56.
Taking another of our principles – Use Their Questions – we zoned in on this statement to test for accuracy. Could 7 x 8 be 56 without us? If so, where was it? Cue arguments involving trees in fields, and even the semantics of the creation story!
r
Where next?
We had to pause for break, but could have easily carried on for hours. Throughout the rest of the day I kept checking in with the pupil who made the proposal. She knew 7 x 8 was somewhere, but couldn’t say where!
As we sought an answer to the original question, we were beginning to explore the concept and nature of Numbers, and so I could have used the 2 Square stimulus from the excellent book “The Philosophy Shop” by Peter Worley of The Philosophy Foundation.
2 2
2 2
How many numbers are on the board?. Peter explains the thinking behind it in his own match-report here.
r
Philosopher in Residence: Two Spaces Left!
We’ve had a fantastic response to our Philosopher in Residence CPD Programme. There’s still a couple of spaces for Autumn Term 2018. Find out more below:
www.thephilosophyman.com/philosopherinresidence
Best wishes,
Tom